Bal-tec™ Home Ball Diameter Calibration
Ball Diameter Calibration
Measurement Approaches
There are a number of acceptable approaches to ball diameter evaluation. To begin with, the sensitivity and accuracy of the equipment used and the cleanliness and environmental control of the surroundings must be commensurate with the accuracy expected.
The driving force for choosing a given procedure is usually based on the availability of the measuring equipment within the organization or by the outside calibration lab doing the work. For most institutions, ball diameter evaluation is only an occasional need so that having dedicated measuring apparatus is not usually practical. The two fundamental approaches to ball size evaluation are “comparative” and “absolute” measurement.
In the comparative approach, a master artifact of known size and quality is compared with the ball under test. The comparative method is much less sensitive to the influence of temperature, as the master and the ball under test are both made of the same material, they are the same size, and they are both exposed to the same environment, so they will expand and contract in unison. In most cases they will both have the same elastic modulus, so the compressive stress of the measuring force will cause the same elastic deformation.
Which master artifact should be used, to set the comparator gage to zero, will usually be determined by expediency. The setting master is never exactly the same size as the ball under test. This leaves us with some dilemmas. The first is that the measuring gage must have sufficient range to span the difference in size between the master and the ball under test. The longer the range of the gage, the lower the sensitivity will be and therefore the accuracy.
A second dilemma is that any lack of linearity, in the scale of the gage, will reflect as a direct error in the measured diameter of the ball under test that must be compensated for. This means that the linearity of the gage scale must be calibrated and certified before the ball diameter measurement will have any value at all. In addition, the measuring force applied by most comparative gages is provided by spring pressure. This means that the measuring force will be lower at the small end of the scale and higher at the large end.
The Hertzian elastic deformations of the ball’s surfaces will vary dramatically with changes in the contact force applied by the measuring gage. Therefore, it is important that any changes in force due to the size difference between the setting master and the ball under test be compensated for. The smaller the ball diameter, the greater the deformation for any given force.
Master Ball
The ideal master artifact would be a very high quality master ball of the same diameter and material as the ball under test. Outside of the gauging equipment, the main factors influencing the error budget of this measurement will be the sphericity and surface texture of both the master ball and the ball under test and the temperature variability. The main problem will be any Delta “T” ( Temperature ) between the two balls. To reduce this to a minimum, the two balls should be placed on a thick aluminum soaking plate with matching spherical cups. Using a tarnished cast iron soaking plate will place the balls at a slightly elevated temperature. The aluminum plate should be at the same elevation as the surface of the gage anvil. This will minimize the effect of any floor to ceiling temperature stratification within the room. The balls must be left together for an extended period to equilibrate (30 minutes per inch).
They should be left uncovered. This point may seem trivial, but on one and five-eighths of an inch ( 1 5/8", 1.625", 41.3 mm ) diameter balls it can amount to three micro inches (75 nanometers) of measuring error in just a few minutes. This amounts to a Delta “T” of a quarter of a degree Fahrenheit.
The bad case scenario goes like this: the covered balls are uncovered and the master ball is immediately measured at least three times and the gage is set to a mean zero (at least five minutes of elapsed time). By this time the ball under test has been exposed to the air currents in the room and will shrink somewhat. This is in contrast with the common idea that the subject will grow, due to the impingement of light energy on the ball. This is one of the real world examples of what actually happens. When is the ball really at 68 °F ( 20 °C )? The ball under test may shrink even more during the time it takes to make three or more measurements (another four to five minutes of elapsed time). Again, on a one and five-eighths inch diameter ball, this can amount to a three micro inch (75 nanometers) change, in this short period (it will take these balls close to an hour to stabilize or equilibrate on the uncovered aluminum soaking plate).
Sphericity
The sphericity of the master calibration ball and that of the ball under test are an important part of the error budget. It doesn’t make any sense; trying to measure a low quality ball with a high quality gage is like trying to measure a brick with a micrometer. I don’t know how many times I have seen calibrated values carried out to the sixth or even seventh decimal place on a commercial quality bearing ball. The typical explanation is that the ball was measured thirty times and the size averaged. I have also seen the reverse where almost perfect balls were measured with a large variability, but it was explained that it didn’t matter because the final size was the average of a lot of measurements. One of these experiences occurred with a world renowned manufacturer of metrology equipment. A really deterministic measurement will not have any outliers, so all measurements should fall within a very narrow pattern, described only by the sphericity of the balls. If you intend to do serious metrology, the first step should be a roundness measurement on at least three orthogonal axii of both the master ball and the ball under test. This will give a reliable check of sphericity. A question that accompanies the sphericity check is an evaluation of the system accuracy of the roundness measurement. The machine, the environment, and the operator all contribute to this uncertainty. (See Plate #1)
Polylobular
We have had innumerable cases where a well measured ball, produced by another company, would not fit into a well measured hole, of larger diameter. This problem goes back to the fact that most balls are produced by a center less grinding process. The balls are rolled between two plates with grooves in them. In addition to rolling, the balls slowly precess. Due to mathematical intricacies in the ratio of ball diameter to groove depth, the balls can also sidell across the width of the groove, creating polylobular, i.e. odd numbers of perfectly geometric three dimensional lobes. These three, five, etc., lobes can be as geometrically perfect as a good ball is spherical. The almost unbelievable fact is that these odd lobes do not show up at all, when measured with a conventional two point gage.
In one extreme case, a set of balls measured consistently the same size within two millionths of an inch (50 nanometers) under a two point gage, when they were actually one and one half thousandths of an inch (almost 40 micrometers), three lobe out of round, when evaluated with a Talyrond.
What is the stated calibration uncertainty (size) of the master ball, and what are the qualifications of the organization providing the certification?
One of the dire consequences of using the comparative method is that the final measurement can never be more accurate than the master artifact and, in fact, can never be quite as good.
Gage Blocks
For the lack of a master ball, a more common form of comparative measurement is to use a wrung up stack of gage blocks to set the gage to zero. (See our paper on gage block wringing procedure on this same site.) This technique allows the master setting gage to be calibrated with reference to the speed of light, so there is very little uncertainty as to the gage block size, but each wringing surface adds to the uncertainty of the overall stack of gage blocks. (A two microinch wringing film is typical of a good wring). It is good shop practice (G.S.P.) to wring tungsten carbide wear blocks to both outer surfaces of a gage block combination. This creates a new disturbance to the intercomparability of the master and the ball under test. Tungsten carbide is four times as stiff as steel, so it will elastically deform less.
We are no longer measuring apples and apples. A whole bunch of variables are introduced when a flat parallel master is used to evaluate a spherical test specimen.
Spherical Gage Tip
Using a spherical gage tip brings up an additional problem. If a typical spherical measuring tip (one-eighth of an inch radius) [3.2mm] is used on the comparator gage, extra problems related to Hertzian elastic deformation will manifest themselves.
The depth that the spherical tip of the measuring machine penetrates the gage block and the amount of flatting that occurs to the spherical gage tip must be calculated. If a diamond spherical tip is used, the minute flatting that occurs can be ignored. Studies indicate the stiffness of diamond to be in the 600,000,000 to 900,000,000 p.s.i. depending on the crystallographic orientation (pounds per square inch) [Young’s modulus] range, so with a normal tip radius and gage pressure, the flattening of the gage tip will be on the order of a nanometer.
This same elastic deformation scenario will also occur to both of the contact surfaces of the ball, and it will be no small matter.
Operator Technique
It always astounds me to see the measuring technician manipulating the ball to be measured forward, then back and side to side under the spherical gage tip by hand. They will tell you that it is too hard and awkward to do it with tweezers and that they do it so fast that the temperature doesn’t have time to effect the measurement, or that they use gloves to insulate their hands from the gage. Well, I’m here to tell you that the heat from their hands will not only affect the present measurement, but it will change any serious measurements made on that gage for the next half hour.
Ball Pattle
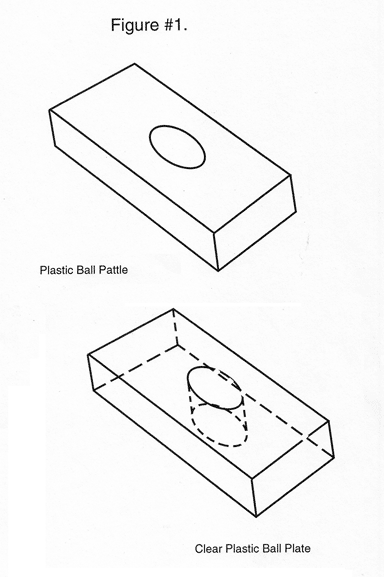
The very simple device used to isolate body temperature from the ball and the gage is a thick piece of acrylic plastic with a close fitting hole through the center. The acrylic plastic is used because it is water clear and it doesn’t have any fillers of any kind that will contaminate the gage environment
If the acrylic plastic isn’t readily available, a paper, linen, or wood-fiber filled plastic can be used by painting the newly machined pattle with clear finger nail polish before use.
Flat Parallel Gage Surfaces
These elastic uncertainties can be reduced but cannot be eliminated by measuring between flat parallel gaging surfaces. The elastic deformation will be much less, but it will still have to be compensated for. The flat parallel measuring approach eliminates the need for peak searching. It will at least halve the gaging time. The measuring accuracy is substantially improved by eliminating the mechanical hysteresis of the gage mechanism, caused by the in and out and side to side wobbling of the ball.
This brings up a new question: how do you get the two measuring surfaces truly flat and parallel, and how do you verify that they are? The usual procedure is to rub, a flat parallel, cast iron, lapping tool whetted with fine diamond compound between the gauging surfaces. This sounds simpler than it is. On a visit to Societe Instruments Physiques SA, in Switzerland, I was told by their lapping expert that it took him one full day to lap the measuring surfaces on one of their machines, flat and parallel.
Adjustable Parallel Gage Tip
It is complicated and difficult, and in my opinion metastable, but some institutions use a very flat measuring tip that is adjusted parallel to the mating flat surface. Any adjustable method that I am familiar with leaves the system in a highly stressed condition. I question the stability, because their operators seem to be constantly tweaking the system.
Breath Shield
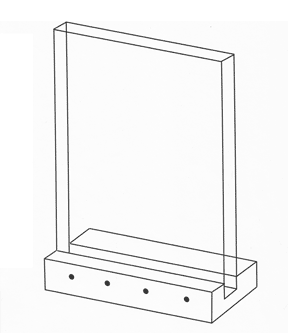
With regard to some more good shop practice (G.S.P.), a breath shield should always be used in front of the gages, if serious measurements are to be made. My favorite design is an in-house version made from a 2x2 inch piece of cold rolled steel that is a foot long. A one-quarter inch wide slot holds a piece of acrylic plastic sixteen inches tall. This is narrow enough to reach your hands around and tall enough to isolate the operator from the gage.
Absolute Method
The second approach to ball diameter calibration is the so-called absolute method. In absolute measurement, temperature is a first order error, that must be held at 68 °F (20 °C) exactly, or any variations must be compensated for.
A micrometer or thread-driven measuring machine is an example of the absolute concept. The accuracy of such a device is basically limited by the accuracy of the screw thread and the ability to interpret the indicating mechanism.
A laser interferometer is an ideal approach for an absolute measuring device. N.I.S.T. uses a multi-color absolute interferometer that has a variable force system. To the best of my knowledge, this is the most accurate sphere evaluation device presently in operation. While we are on this subject, a quick discussion of their approach isn’t out of our realm. The balls are first measured approximately (within one light band or 10 microinches [.025 micrometers] ), by conventional means. The subject ball is put in the instrument and measured, three times, with the three different bands (colors) of cadmium and two bands of mercury, under the first force. The same readings are then repeated under two different forces, and the absolute size at zero force is extrapolated. One of the results of this work is that the mathematical algorithms for calculating Hertzian elastic deformation developed by the CSIRO in Australia have been verified to the letter. You should be aware that outside of the applied force, the two main factors effecting elastic deformation are Young’s Modulus of elasticity and Poisson’s ratio, neither one of which are actually known to better than plus or minus 10%.
Laser Scales
The final and by far the most practical approach to absolute ball diameter measurement are the modern laser scale devices being produced today. They have sub-micro inch calibration and repeatability and they are quite temperature tolerant. Flat, parallel measuring surfaces should be used without question.
Liquid Bath
It is common practice for the balls awaiting measurement to be placed into a liquid bath of water or water-based fluid. The assumption here is that a liquid bath placed in a temperature controlled room will assume the temperature of the room. This is wrong! Any decent lab will have a relative humidity of 50% or less, and it is often far less. This low humidity leads to serious evaporation from the surface of the liquid bath, with an accompanying drop in bath temperature. Even when a constant temperature bath is used, there will be a serious temperature drop when the ball is dried for measurement. I do not approve of liquid soaking for any serious measurement.
It is often recommended that the quality of the flat parallel surfaces of the gage be evaluated using a parallel optical flat which is illuminated with monochromatic light. This is a good story line, but I have yet to find a single technician that actually does this. For the most part, this is a good fairy tale to get an evaluator off your back. Where do you get a good enough optical device that is flat and parallel enough and how do you get it certified? How do you pump enough monochromatic light down through and up through the optical flat when, at best, 17% of the light is reflected from the glass surfaces? The ball measuring machine is not a small micrometer that you can easily manipulate under the monochromatic light source.
How do you factor in elastic compliance (deformation) between the four interfaces that are bound to occur? By using a metal coated optical parallel and a powerful (125 watts) mercury light source. This technique can be forced to work, but it is not at all practical, nor is it that accurate.
Years ago when we were perfecting our measuring techniques, we built a Fizeau micro interferometer (40x) with the attitude of the test plate positioned parallel to a three ball kinematic platform. This device was very tedious to use, but it did work well, and it provided us with an absolute traceable standard to work from.
The effective way to check the flatness and parallelism of the surfaces is to measure the diameter of a small (0.25", 1/4 inch or 6 mm ), very high quality ball. This ball is held captive, so that it can’t turn around in the pattle like handle. The distance between the surfaces is measured in at least five places.
Place the ball in the center between the surfaces and set the gage to zero. Now measure as far forward as possible, then as far back as possible, then off to the left side and then the right. This is a stringent test, as every micro inch of flatness error in each surface will cause a two micro inch difference in the measurement of the ball diameter.
We actually profile the measuring gap between the two surfaces every three thousandths of an inch in both the “X” and “Y” axii using special in-house tooling.
It is typical of the parallel lapping process, to generate a slightly positive (convex) surface. Two factors contribute to this condition. When the lapping tool (parallel cast iron disk moves, there will be a hydrodynamic wedge of liquid built up at the trailing edge. The cast iron lap has a Young’s Modulus of Elasticity (stiffness) of only 18 million p.s.i. A small diameter measuring tip at a high gage pressure will elastically dent the cast iron lap, and there will be a dynamic flow of the metallic cast iron around the tip, further exacerbating the problem. Nothing is perfectly rigid and this goes for the stem of the measuring machine, too. The bending or flexing of the stem or stems of the gage will also contribute to the convexity of the gage tip or tips. I had to take a trip to the Heidenhain facility in Germany to fully appreciate the implications of this problem.
The fluid film hydrodynamic wedge can be greatly reduced by finishing the final polish dry, but the lap will still tilt on the air wedge that will be developed by the movement. The cutting action of a dry lap is so extremely slow that you should only plan on removing a few micro inches (75 nanometers) with this technique.
The very best flatness and parallelism that is practical to achieve is two micro inches (50 nanometers). If you can manage to measure the ball near the center of the measuring tip, every time, this error will nearly vanish.
There are dodges that can be used to improve the gauging accuracy an order of magnitude or two. Build a gantry shaped frame for the gage instead of a conventional “C” frame (this will dramatically reduce deflection and will eliminate gage frame hysteresis). You can build the entire gage frame out of Invar™. This will eliminate any effect of temperature change. Place the gage on a vibration isolated air table and surround the gage with 5 inch (127mm) thick blocks of aluminum. They will act as a heat sinks or more accurately a thermal phase shifting system, with a very long time constant.
An example of how all of this actually works occurred recently in our facility. A customer wanted a master set of tantalum balls from 0.0153" to 0.0157", ( inches), (0.39 mm ) diameter. A selection of these balls was calibrated on an absolute laser scale measuring machine that was primarily dedicated to evaluating miniature balls. The gage was programmed to read out in 0.2 micro inches (5 nanometer increments). The full set of balls was measured and the raw data was rounded off to the nearest micro inch. The set of balls were given to a second technician and measured again on another machine of the same make, programmed to meet the same parameters. I was called by the technician who was in a minor panic. Every one of the balls had measured exactly 12 microinches smaller than the first set of measurements. I smiled to myself, and told him that was great. After he freaked out, I told him that the measuring machine setup for the miniature balls, had a micro grain hot isostatic pressed Tungsten Carbide ( T.C.) anvil and the second machine in the main lab had an anvil of vacuum melted chrome alloy steel. The T.C. anvil had a Young’s Modulus of 112 million p.s.i. ( pounds per square inch ) [tungsten carbide has a higher Young’s Modulus of Elasticity in compression than it does in tension] and the chrome alloy steel was only 30 million p.s.i., therefore 12 micro inches on a 0.015 inch (0.39mm) diameter, tantalum ball was exactly what they should have measured. These measurements hadn’t had any correction for Hertzian elastic deformation applied yet.
How Close Can You Measure
One of the goals of this little essay is to point out the myriad of error sources that contribute to the true error budget for ball size evaluation. How accurately can you possibly measure the diameter of an instrument grade ball that is ten millionths of an inch (0.25 micrometers) out of round, with undulations in the surface texture of an additional three micro inches (75 nanometers)?
Using an enhanced Talyrond, we are comfortable with an uncertainty of plus or minus one micro inch (25 nanometers) for the measurement of sphericity.
Using our Ultra-Spherometer, we can evaluate the sphericity of a one inch diameter metallic ball with an uncertainty of plus or minus one nanometer, but it takes a full eleven hours, and that’s after a twenty-four hour soaking period. We published a paper on this procedure in the Precision Engineering Journal of the A.S.P.E.
Absolute size is a much fuzzier situation. To begin with, the uncertainty of the sphericity is no better than two microinches (50 nanometers). The readout and the repeatability of the laser scale measuring machine is 0.2 microinches (5 nanometers), but the overall accuracy of the entire gage is more like three microinches. Without using a lot of witchcraft with look up tables and crossed fingers, we feel that three microinches is a realistic figure, just for the gage.
We have actually measured full sets of extremely high quality balls that were calibrated with the N.I.S.T. absolute interferometer to within the three microinch envelope. When you add some temperature variation and an operator, we feel that 10 microinches is a totally realistic commercial uncertainty, and I don’t think that too many commercial labs can actually do as well.
Some afterthoughts:
- The balls under test should be demagnetized prior to cleaning.
- The balls must obviously be very clean and dry. Ultrasonic cleaning is recommended.
- Handle the balls under test only with tweezers or a vacuum wand.
- The soaking plate can be combined into a clean room quality, covered transport container.
- When using a master ball, to set the gage it is a good policy to mark it with a drop of paint or other identification. It is too easy to mix the balls.
- It is always a good policy for the technician to wear clean room gloves (not cotton), and some form of lint free clothing.
